Transistor-Transistor Logic (TTL)

Transistor-Transistor Logic, or TTL, refers to the technology for designing and fabricating digital integrated circuits that employ logic gates consisting primarily of bipolar transistors. It overcomes the main problem associated with DTL, i.e., lack of speed.

The input to a TTL circuit is always through the emitter(s) of the input transistor, which exhibits a low input resistance. The base of the input transistor, on the other hand, is connected to the Vcc line, which causes the input transistor to pass a current of about 1.6 mA when the input voltage to the emitter(s) is logic '0', i.e., near ground. Letting a TTL input 'float' (left unconnected) will usually make it go to logic '1', but such a state is vulnerable to stray signals, which is why it is good practice to connect TTL inputs to Vcc using 1 kohm pull-up resistors.

The most basic TTL circuit has a single output transistor configured as an inverter with its emitter grounded and its collector tied to Vcc with a pull-up resistor, and with the output taken from its collector. Most TTL circuits, however, use a totem pole output circuit, which replaces the pull-up resistor with a Vcc-side transistor sitting on top of the GND-side output transistor. The emitter of the Vcc-side transistor (whose collector is tied to Vcc) is connected to the collector of the GND-side transistor (whose emitter is grounded) by a diode. The output is taken from the collector of the GND-side transistor. 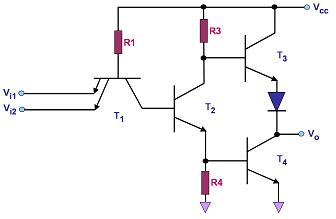Figure 1 shows a basic 2-input TTL NAND gate with a totem-pole output.

Figure 1. A 2-input TTL NAND Gate with a Totem Pole Output Stage

In the TTL NAND gate of Figure 1, applying a logic '1' input voltage to both emitter inputs of T1 reverse-biases both base-emitter junctions, causing current to flow through R1 into the base of T2, which is driven into saturation. When T2 starts conducting, the stored base charge of T3 dissipates through the T2 collector, driving T3 into cut-off. On the other hand, current flows into the base of T4, causing it to saturate and pull down the output voltage Vo to logic '0', or near ground. Also, since T3 is in cut-off, no current will flow from Vcc to the output, keeping it at logic '0'. Note that T2 always provides complementary inputs to the bases of T3 and T4, such that T3 and T4 always operate in opposite regions, except during momentary transition between regions.

On the other hand, applying a logic '0' input voltage to at least one emitter input of T1 will forward-bias the corresponding base-emitter junction, causing current to flow out of that emitter. This causes the stored base charge of T2 to discharge through T1, driving T2 into-cut-off. Now that T2 is in cut-off, current from Vcc will be diverted to the base of T3 through R3, causing T3 to saturate. On the other hand, the base of T4 will be deprived of current, causing T to go into cut-off. With T4 in cut-off and T3 in saturation, the output Vo is pulled up to logic '1', or closer to Vcc.

Outputs of different TTL gates that employ the totem-pole configuration must not be connected together since differences in their output logic will cause large currents to flow from the logic '1' output to the logic '0' output, destroying both output stages. The output of a typical TTL gate under normal operation can sink currents of up to 16 mA.

The noise margin of a logic gate for logic level '0', Δ0, is defined as the difference between the maximum input voltage that it will recognize as a '0' (Vil) and the maximum voltage that may be applied to it as a '0' (Vol of the gate driving it). For logic level '1', the noise margin Δ1 is the difference between the minimum input voltage that may be applied to it as a '1' (Voh of the gate driving it) and the minimum input voltage that it will recognize as a '1' (Vih). Mathematically, Δ0 = Vil-Vol and Δ1 = Voh-Vih. Any noise that causes a noise margin to be overcome will result in a '0' being erroneously read as a '1' or vice versa. In other words, noise margin is a measure of the immunity of a gate from reading an input logic level incorrectly. For TTL, Vil = 0.8V and Vol = 0.4V, so Δ0 = 0.4V, and Voh = 2.4V and Vih = 2.0 V, so Δ1 = 0.4V. These noise margins are not as good as the noise margins exhibited by DTL.

As mentioned earlier, TTL has a much higher speed than DTL. This is due to the fact that when the output transistor (T4 in Figure 1) is turned off, there is a path for the stored charge in its base to dissipate through, allowing it to reach cut-off faster than a DTL output transistor. At the same time, the equivalent capacitance of the output is charged from Vcc through T3 and the output diode, allowing the output voltage to rise more quickly to logic '1' than in a DTL output wherein the output capacitance is charged through a resistor.

The commercial names of digital IC's that employ TTL start with '74', e.g., 7400, 74244, etc. Most TTL devices nowadays, however, are named '74LSXXX', with the 'LS' standing for 'low power Schottky'. Low power schottky TTL devices employ a Schottly diode, which is used to limit the voltage between the collector and the base of a transistor, making it possible to design TTL gates that use significantly less power to operate while allowing higher switching speeds. See also: CMOS circuits.

See Also: TTL Parameters; Logic Gates; RTL; DTL; CMOS

HOME