Digital Logic Gates

Digital logic gates, which are also known as combinational logic gates or simply 'logic gates', are digital IC's whose output at any time is determined by the states of its inputs at that time. Since logic gates are digital IC's, their input and output signals can only be in one of two possible digital states, i.e., logic '0' or logic '1'. Thus, the logic state in which the output of a logic gate will be put in depends on the logic states of each of its individual inputs.

The primary application of logic gates is to implement 'logic' in the flow of digital signals in a digital circuit. Logic in its ordinary sense is defined as a branch of philosophy that deals with what is true and false, based on what other things are true and false. This essentially is the function of logic gates in digital circuits - to determine which outputs will be true or false, given a set of inputs that can either be true (logic '1') or false (logic '0').

The response output (usually denoted by Q) of a logic gate to any combination of inputs may be tabulated into what is known as a truth table. A truth table shows each possible combination of inputs to a logic gate and the combination's corresponding output. Table 1, which describes the various types of logic gates, provides a truth table for each of them as well.

Interestingly, the operation of logic gates in relation to one another may be represented and analyzed using a branch of mathematics called Boolean Algebra which, like the common algebra, deals with manipulation of expressions to solve or simplify equations. Expressions used in Boolean Algebra are called, well, Boolean expressions.

Table 1. Logic Gates and their Properties

Gate

Description

Truth Table

AND Gate

The AND gate is a logic gate that gives an output of '1' only when all of its inputs are '1'. Thus, its output is '0' whenever at least one of its inputs is '0'. Mathematically, Q = A · B.

A	B	Output Q
0	0	0
0	1	0
1	0	0
1	1	1

OR Gate

The OR gate is a logic gate that gives an output of '0' only when all of its inputs are '0'. Thus, its output is '1' whenever at least one of its inputs is '1'. Mathematically, Q = A + B.

A	B	Output Q
0	0	0
0	1	1
1	0	1
1	1	1

NOT Gate

The NOT gate is a logic gate that gives an output that is opposite the state of its input. Mathematically, Q = A.

A	Output Q
0	1
1	0

NAND Gate

The NAND gate is an AND gate with a NOT gate at its end. Thus, for the same combination of inputs, the output of a NAND gate will be opposite that of an AND gate. Mathematically, Q = A · B.

A	B	Output Q
0	0	1
0	1	1
1	0	1
1	1	0

NOR Gate

The NOR gate is an OR gate with a NOT gate at its end. Thus, for the same combination of inputs, the output of a NOR gate will be opposite that of an OR gate. Mathematically, Q = A + B.

A	B	Output Q
0	0	1
0	1	0
1	0	0
1	1	0

EXOR Gate

The EXOR gate (for 'EXclusive OR' gate) is a logic gate that gives an output of '1' when only one of its inputs is '1'.

A	B	Output Q
0	0	0
0	1	1
1	0	1
1	1	0

There are several kinds of logic gates, each one of which performs a specific function. These are the: 1) AND gate; 2) OR gate; 3) NOT gate; 4) NAND gate; 5) NOR gate; and 6) EXOR gate. Table 1 above presents these and their characteristics.

Logic gates may be thought of as a combination of switches. For instance, the AND gate, whose output can only be '1' if all its inputs are '1', may be represented by switches connected in series, with each switch representing an input. All the switches need to be activated and conducting (equivalent to all the inputs of the AND gate being at logic '1'), for current to flow through the circuit load (equivalent to the output of the AND gate being at logic '1').

An OR gate, on the other hand, may be represented by switches connected in parallel, since only one of these parallel switches need to turn on in order to energize the circuit load.

In Boolean Algebra, the AND operation is represented by multiplication, since the only way that the result of multiplication of a combination of 1's and 0's will be equal to '1' is if all its inputs are equal to '1'. A single '0' among the multipliers will result in a product that's equal to '0'. The Boolean expression for 'A AND B' is similar to the expression commonly used for multiplication, i.e., A·B.

The OR operation, on the other hand, is represented by addition in Booelean Algebra. This is because the only way to make the result of the addition operation equal to '0' is to make all the inputs equal to '0', which basically describes an 'OR' operation. The Boolean expression for 'A OR B' is therefore A+B.

The NOT operation is usually denoted by a line above the symbol or expression that is being negated: A = NOT(A). The NAND operation is simply an AND operation followed by a NOT operation. The NOR operation is simply an OR operation followed by a NOT operation. The symbols used for logic gates in electronic circuit diagrams are shown in Figure 1.

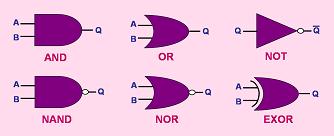Figure 1. Logic Gate Symbols

One of the most useful theorems used in Boolean Algebra is De Morgan's Theorem, which states how an AND operation can be converted into an OR operation, as long as a NOT operation is available. De Morgan's Theorem is usually expressed in two equations as follows:

(A·B) = A + B; and

(A+B) = A · B.

De Morgan's Theorem has a practical implication in digital electronics - a designer may eliminate the need to add more IC's to the design unnecessarily, simply by substituting gates with the equivalent combination of other gates whenever possible. Since NAND and NOR gates can be used as NOT gates, de Morgan's Theorem basically implies that any Boolean operation may be simulated with nothing but NAND or NOR gates. This is why NAND and NOR gates are also called universal gates.

See Also: RTL / DTL / TTL; Boolean Algebra

HOME