Statistical Process Control (SPC) is a system for monitoring, controlling, and improving a process through statistical analysis. It has many aspects, from control charting to process capability studies and improvement. Nonetheless, the over-all SPC system of a company may be broken down into four basic steps: 1) measuring the process; 2) eliminating variances within the process to make it consistent; 3) monitoring the process; and 4) improving the process. This four-step cycle may be employed over and over again for continuous improvement.

Bulk of SPC concepts in use today were developed based on the premise that the process parameter being controlled follows a normal distribution. Any SPC practitioner must be aware that the parameter must first be confirmed to be normal before being subjected to analysis concepts based on normal behavior. Thus, any discussion on SPC must be preceded by a discussion of what a normal distribution is. 

The Normal Distribution

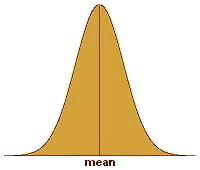
The normal distribution (see Fig. 1), normal curve, or bell-shaped curve, is probably the most recognized and most widely-used statistical distribution.  The reason for this is that many physical, biological, and social parameters obey the normal distribution. Such parameters are then said to behave 'normally' or, more simply, are said to be 'normal.'  The semiconductor industry has many processes that output data or results that comprise a normal distribution.  As such, it is important for every process engineer to have a firm grasp of what a normal distribution is.

Aside from the fact that the normal distribution is frequently encountered in our day-to-day lives, the mathematics governing normal behavior are fairly simple.  In fact, only two parameters are needed to describe a normal distribution, namely, the mean or its center, and the standard deviation (also known as sigma) or its variability. Knowing both parameters is equivalent to knowing how the distribution looks like.

The normal distribution is bell-shaped, i.e., it peaks at the center and tapers off outwardly while remaining symmetrical with respect to the center.  To illustrate this in more tangible terms, imagine taking down the height of every student in a randomly selected Grade 5 class and plotting the measurements on a chart whose x-axis corresponds to the height of the student and whose y-axis corresponds to the number of students.

Figure 1. The Normal Distribution

   

What is expected to emerge from this exercise is a normal curve, wherein a big slice of the student population will have a height that is somewhere in the middle of the distribution, say 57-59 inches tall.  The number of students belonging to other height groups will be less than the number of students in the 57"-59" category.

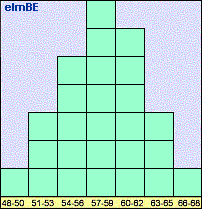
In fact, the number of students decreases at a calculable rate as the height group moves further away from the center. Eventually you might find only one shortest student at, say, 48", and one tallest student who probably stands at 66". Lastly, plotting the number of the students falling under different height ranges of equal intervals will result in a bell-shaped curve. Such a plot is called a histogram, a simple example of which is shown in Figure 2.

What's notable about normal distributions is that regardless of their standard deviation value,  the % of data falling under a given number of standard deviations is constant.  For example, say that the standard deviation of process 1 is 100, and the standard deviation of process 2 is 200.  Process 1 and Process 2 will have different data distribution shapes (Process 1 being more stable), but for both processes, 66% of the data under the normal curve will fall within +/- one (1) standard deviation from the mean of the distribution (i.e., between {mean - 1 sigma} and {mean + 1 sigma}), and 37% of the data will be outside it. Table 1 shows the percentages of data falling under different numbers of sigma.

Table 1. % Data Falling Under Different Numbers of +/- Sigma

Skewed Distributions

Perfectly normal curves are hard to come by with finite samples or data. Thus, some data distributions that are theoretically normal may not appear to be one once the data are plotted, i.e., the mean may not be at the center of the distribution or there may be slight non-symmetry. If a normal distribution appears to be 'heavy' or leaning towards the right side of the distribution, it is said to be skewed to the left.  A normal distribution that's leaning to the left is said to be skewed to the right.

Many response parameters encountered in the semiconductor industry behave normally, which is why statistical process control has found its way extensively into this industry.  The objective of SPC is to produce data distributions that are stable, predictable, and well within the specified limits for the parameter being controlled.

In relation to the preceding discussions, this is equivalent to achieving data distributions that are centered between the specified limits, and as narrow as possible. Good centering between limits and negligible variation translates to parameters that are always within specifications, which is the true essence of process control.

Control Charting

It is often said that you can not control something that you do not measure.  Thus, every engineer setting up a new process must have a clear idea of how the performance of this new process is to be measured.  Since every process needs to satisfy customer requirements, process output parameters for measurement and monitoring are generally based on customer specifications.  Industry-accepted specifications are also followed in selecting process parameters for monitoring. 

Control charting is a widely-used tool for process monitoring in the semiconductor industry.  It employs control charts (see Fig. 3), which are simply plots of the process output data over time.  Before a control chart may be used, the process engineer must first ensure that the process to be monitored is normal and stable. 

A process may have several control charts - one for each of its major output parameters. A new control chart must have at least the following:  the properly labeled x- and y-axes, lines showing the lower and upper specification limits for the parameter being monitored, and a line showing the center or target of these specifications.  Once a control chart has been set up, the operator must diligently plot the output data at predefined intervals.

After 30 data points have been collected on the chart (may be less if measurement intervals are long), the upper and lower control limits of the process may already be computed.  Control limits define the boundaries of the normal behavior of the process.  Their values depend only on the output data generated by the process in the immediate past. Control limits are therefore independent of specification limits. However, both sets of limits are used in the practice of SPC, although in different ways.

The lower control limit LCL and the upper control limit UCL of a process may be calculated from the mean and standard deviation (or sigma) of the plotted data as follows:

LCL = Mean - (3 x Sigma);

UCL = Mean + (3 x Sigma).

Thus, the span from the LCL of a process to its UCL is 6 sigma.  The probability of getting points outside this +/- 3 sigma range is already very low (see Table 1).  Getting a measurement outside this range should therefore warn an engineer that something abnormal is happening, i.e., the process may be going out of control.  This is the reason why these boundaries are known as 'control limits.'

Once the control limits have been included on the control charts (also in the form of horizontal lines like the specification limits), the operator can start using the chart visually to detect anomalous trends in the process that she would need to notify the engineer about. 

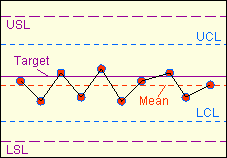
Figure 3. Example of a control chart showing data that are

slightly off-centered, but nonetheless in control and within specs

For instance, any measurement outside the control limits is an automatic cause for alarm, because the probability of getting such a measurement is low.  Four (4) or more consecutively increasing or decreasing points form a trend that is not normal, and therefore deserves attention.  Six (6) consecutive points on one side of the mean also deserve investigation. When such abnormalities are observed, the process owner must take an action to bring the process back to its normal behavior.

Control limits must be recomputed regularly (say, every quarter), to ensure that the control limits being used by the operator are reflective of the current process behavior.  

Read more about: Control Charting.

The Process Capability Indices

Being able to monitor a process for out-of-control situations is one thing; knowing how a process actually performs is another. Eyeballing the centering and shape of a data distribution can give us quick, useful information on how the corresponding process behaves, but it is not very helpful in quantifying the process' actual and potential performance.  It is for this reason that statisticians have come up with methods for  expressing the behavior or capability of process distributions in terms of single numbers known as process capability indices.

Process capability refers to the ability of a process to meet customer requirements or specification limits, i.e., how consistent its output is in being within its lower and upper spec limits.  A process capability index should therefore be able to indicate how well the process can meet its specs.

The most basic process capability index is known as the simple process capability index, denoted by 'Cp'. Cp quantifies the stability of a process, i.e., the consistency of its output.  As mentioned earlier, the process capability indices discussed here presume the normality of the process.  As such, the inconsistency of the process may be measured in terms of the standard deviation or sigma of the output data of the process.  This is what Cp does - it uses the sigma to quantify the variation of a process, and compares it against the distance between the upper spec limit (USL) and lower spec limit (LSL) of the process.  In mathematical form:  Cp = (USL - LSL) / (6 x Sigma).

The quantity (USL - LSL) is basically the range of output that the process must meet, while 6 sigma corresponds to +/- 3 sigma from the mean, or 99.73% of all the process output data.   The smaller the value of 6 sigma, the narrower the process output distribution is, denoting higher stability.  Thus, Cp increases as process stability increases. Thus, a process needs a Cp > 1 to ensure that it is narrow enough to meet the spec range 99.73% of the time.

Although Cp indicates the stability of a process, it has one major drawback that makes it almost useless in the semiconductor industry. It does not consider the centering of the process distribution within the spec limits.  A process with a Cp of 100 may be very stable, with all its output data very close to each other, but it may also be out-of-spec at all times, i.e., if it is centered outside the spec limits! 

This weakness of Cp is addressed by another process capability index, Cpk. Cpk measures how centered the output of the process is between its lower and upper limits, as well as how variable the output is.  Cpk is expressed as the ratio of how far the mean of the output data is from the closer spec limit (the centering of the process) to three times their standard deviation (the process variability).

C_PL = (mean - LSL) / (3 sigma) : process capability index for single-sided (lower) spec limit

C_PU = (USL - mean) / (3 sigma) : process capability index for single-sided (upper) spec limit

Cpk = min{C_PL,C_PL} : process capability index for two-sided spec limits  

What these formulae mean is this: Cpk is equal to whichever is lower between C_PL and C_PU.  If the mean of the process data is closer to the lower spec limit LSL, then Cpk = C_PL. If the mean of the process data is closer to the upper spec limit USL, then Cpk = C_PU.

An ideal process is one whose output is always dead center between the spec limits, such that the mean of its output data equals this dead center and the standard deviation is zero.  The Cpk of this ideal process is infinite (so is the Cpk of other processes whose sigma = 0, as long as the LSL<mean<USL).

The Cpk decreases if one or both of the following occurs:  1) the data become less centered; and 2) the data become more variable (sigma increases).  Thus, improving the process capability of a process entails one or both of: 1) centering the output between limits and 2) decreasing the variation of the output data.

The essence of SPC, therefore, is being able to recognize whether a low Cpk is due to the mean of the process or its sigma, and taking the necessary actions to correct the problem, be it centering of the data or making them less variable.  In any process, the actions needed to center the output data may be different from what needs to be done to make the data less variable.  Knowledge of this basic SPC principle is therefore a necessary weapon in every process engineer's arsenal.

As of this writing, most semiconductor companies target a Cpk of 1.67 for their processes, although they would be satisfied to have an actual Cpk of at least 1.33.  Everything, of course, depends on what spec limits the customer imposes on the manufacturer.  Still, at the end of the day it should always be the manufacturer's goal to center their output between these spec limits as consistently as possible.