Digital-to-Analog Converters (DAC's)

A digital-to-analog converter, or simply DAC, is a semiconductor device that is used to convert a digital code into an analog signal.  Digital-to-analog conversion is the primary means by which digital equipment such as computer-based systems are able to translate digital data into real-world signals that are more understandable to or useable by humans, such as music, speech, pictures, video, and the like.  It also allows digital control of machines, equipment, household appliances, and the like.

A typical digital-to-analog converter outputs an analog signal, which is usually voltage or current, that is proportional to the value of the digital code provided to its inputs. Most DAC's have several digital input pins to receive all the bits of its input digital code in parallel (at the same time).  Some DAC's, however, are designed to receive the input digital data in serial form (one bit at a time), so these only have a single digital input pin. 

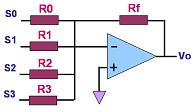
A simple DAC may be implemented using an op-amp circuit known as a summer, so named because its output voltage is the sum of its input voltages. Each of its inputs uses a resistor of different binary weight, such that if R₀=R, then R₁=R/2, R₂=R/4, R₃=R/8,.., R_N-1=R/(2^N-1).  The output of a summer circuit with N bits is:    

Vo = -V_R (Rf / R) (S_N-12^N-1 + S_N-22^N-2+...+S₀2⁰) where V_R is the voltage to which the bit is connected when the digital input is '1'. A digital input is '0' if the bit is connected to 0V (ground).   A 4-bit summer circuit is shown in Figure 1.

Figure 1.  An Op Amp Summer Circuit Used as a DAC; where R0 = 2 R1 = 4 R2 = 8 R3

One problem with this circuit is the wide range of resistor values needed to build a DAC with a high number of digital inputs.  Putting thin-film resistors that come in a wide range of values (e.g., from a few kΩs to several MΩs) on a single semiconductor chip can be very difficult, especially if high accuracy and stability are required.

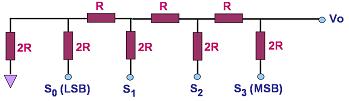
A better-designed and more commonly-used circuit for digital-to-analog conversion is known as the R-2R ladder DAC, a 4-bit version of which is shown in Fig. 2.  It consists of a network of resistors with only two values, R and 2R.  The input S_N to bit N is '1' if it is connected to a voltage V_R and '0' if it is grounded. Thevenin's Theorem may be applied to prove that the output Vo of an R-2R ladder DAC with N bits is:

Vo =   V_R/2^N (S_N-12^N-1 + S_N-22^N-2+...+S₀2⁰).

Thus, the output of the R-2R ladder in Figure 2 is Vo = V_R/2⁴ (S₃2³+S₂2²+S₁2¹+S₀2⁰) or Vo = V_R (S₃ / 2 + S₂ / 4 + S₁ / 8 + S₀ / 16) . In effect, contribution of each bit to the analog output is proportional to its binary weight.

Figure 2.  A 4-bit R-2R Ladder DAC

See also:  DAC Parameters; ADC's; Op Amps