Test Yield Models

Test Yield is the ratio of the number of devices that pass electrical testing to the total number of devices subjected to electrical testing, usually expressed as a percentage (%).  All semiconductor companies aim to maximize their test yields, since low test yields mean throwing away a large number of units that have already incurred full manufacturing costs from wafer fabrication to assembly. The major causes of yield loss are processing problems, product design limitations, and random point defects in the circuit. 

Examples of processing problems that could lead to low yields include: 1) excessive variations in the oxide thickness; 2) excessive variations in doping, which can cause high resistances in some areas; 3) masking alignment problems; 4) ionic contamination; and 5) excessive variations in the polysilicon layer thickness, which can result in over-etched poly gates that cause transistors to malfunction.

Poor design of products will also lead to low test yields, manifesting as oversensitive devices that fail at the slightest hint of process or operational variation. However, not all circuit sensitivity issues may be attributed solely to improper product design. In some instances, limitations in the design technology itself simply can not compensate for parameter variability inherent to wafer fab processes. For instance, variations in substrate doping, ion implant dosage, and gate oxide thickness can affect the threshold voltage of MOS devices.

Even if the product is properly designed and no processing problems are encountered, a lot may also exhibit test yield issues as a result of the presence of point defects on the wafer.  Point defects are usually due to dust or particulate contamination in the environment or equipment issues where the wafer was processed.  Point defects may also be due to crystallographic imperfections within the silicon wafer itself.

Yield loss mechanisms must be understood in order to keep manufacturing costs in control, evaluate process capabilities better, and predict the performance of future products.  To understand yield loss mechanisms, these are mathematically expressed in terms of 'yield models', which are equations that translate defect density distributions into predicted yields. Examples of yield models used by IC manufacturers are the Poisson Model, the Murphy Model, the Exponential Model, and the Seeds Model.

Choosing a yield model is usually done based on the actual data being experienced by the IC manufacturer.  Yield  data from a specific fab process, for instance, may be analyzed per die size and compared to results predicted by the various models.  The model that provides a best fit for the data may be adopted for use in subsequent yield analyses.

One simple yield model assumes a uniform density of randomly occurring point defects as the cause of yield loss. If the wafer has a large number of chips (N) and a large number of randomly distributed defects (n), then the probability Pk that a given chip contains k defects may be approximated by Poisson's distribution, or Pk = e^-m (m^k/k!) where m = n/N.  The yield Y is the probability that a chip has no defects (k=0), so Y = e^-m.  If D is the chip defect density, then D = n/N/A = n/NA where A is the area of each chip.  Since m=n/N, then m, which is the average number of defects per chip, is AD. Thus, Y = e ^(-AD), which is the Poisson Yield Model.

Many experts believe that the Poisson Model is too pessimistic, since defects are often not randomly distributed, but rather clustered in certain areas.  Defect clustering allows less defects over large areas of the wafer than if the defects are randomly and uniformly distributed.

A simple model that assumes a non-uniform distribution of defects gives the yield Y as: Y= ₀∫^∞ e ^(-AD) f(D) dD, where f(D) is the distribution of the defect density.  Assuming a triangular defect density distribution as shown in Figure 1a, Y = [(1-e^(-AD))/(AD)]². This is Murphy's Yield Model.  For a rectangular defect density distribution as shown in Fig. 1b, Y = (1-e^(-2AD))/(2AD). Many experimental data fit this last equation, where the defect density is assumed to be rectangular.

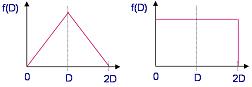
Figure 1. Triangular (left) and Rectangular (right)

Defect Density Distributions

Another yield model is the Exponential Yield Model, which assumes that high defect densities are restricted to small regions of the wafer. Thus, the exponential yield model is best applied to instances wherein severe defect clustering is observed. The yield Y using this model is expressed as follows: Y = 1/(1+AD).  Lastly, the Seeds Model gives the following equation for yield: Y = e^-√(AD).

Rejoinder:  This article is currently under review in response to the following email.  Our thanks to the email sender.

Dear EESemi,
 
I happened to come across your site while Google searching for yield models.  You have a nice, one-page summary for yield models.
 
However, there is one obscure error.  You refer to Gordon Moore's yield model (Y = e-?(AD)) as "the Seeds Model" and don't give Seeds credit for the model that is his, Y = 1/(1+AD), which you call the exponential yield model.
 
Another yield model is the Exponential Yield Model, which assumes that high defect densities are restricted to small regions of the wafer. Thus, the exponential yield model is best applied to instances wherein severe defect clustering is observed. The yield Y using this model is expressed as follows: Y = 1/(1+AD).  Lastly, the Seeds Model gives the following equation for yield: Y = e-?(AD).
 
Gordon Moore presented the Y = e-?(AD) model as an empirical model I believe in his 1970 Electronics article, "What Level of LSI is Best For You." 
 
R.A. Seeds should also be credited with what is now called the Bose-Einstein yield model, Y = 1/(1+AD)^k, where k is a layer-dependent factor. In a "Letters" article he wrote, he said that his simple Y = 1/(1+AD) model could be extended to accommodate additional critical layers and even proposed Y = 1/(1+AD)^3, given that there were typically only 3 critical layers at the time (Active, Gate, Metal interconnect).  This has just been extended to more layers (higher "k") as semiconductor technology became more complex.
 
I don't know how this error got started.   Gordon Moore happened to mention in this paper that his empirical model approximated the Seeds yield model in the low yield region.  This low yield region is where most of his data was and where "advanced" circuits at the time were being developed and needed the modeling.
 
The first printed example I've seen of the error in calling his model the "Seeds" model was a 1982 Technology Associates tutorial (O.D. "Bud" Trapp).
 
It would be nice to see this cleared up instead of being propagated like an internet urban legend.  Unfortunately, one must go to the library to see the original sources.
 

Thank you.
 
Best Regards,
Kimo Cummings            

Home

Copyright © 2005. EESemi.com. All Rights Reserved.