Scatter Diagram

The Scatter Diagram is a tool for determining the potential correlation between two different sets of variables, i.e., how one variable changes with the other variable.

This diagram simply plots pairs of corresponding data from two variables, which are usually two variables in a process being studied. The scatter diagram does not determine the exact relationship between the two variables, but it does indicate whether they are correlated or not. It, by itself, also does not predict cause and effect relationships between these variables.

The scatter diagram is used to: 1) quickly confirm a hypothesis that two variables are correlated; 2) provide a graphical representation of the strength of the relationship between two variables; and 3) serve as a follow-up step to a cause-effect analysis to establish whether a change in an identified cause can indeed produce a change in its identified effect.

To make a scatter diagram for two variables requiring confirmation of correlation, the following simple steps are usually followed:

1) collect 50-100 pairs of data for the two variables and tabulate them;

2) draw the x- and y-axes of the diagram, along with the scales that increase to the right for the x-axis and upward for the y-axis;

3) assign the data for one variable to the x-axis (the independent variable) and the data for the other variable to the y-axis (the independent variable);

4) plot the data pairs on the scatter diagram, encircling (as many times as necessary) all data points that are repeated.

Interpretation of the resulting scatter diagram is as simple as looking at the pattern formed by the points. If the data points plotted on the scatter diagram are all over the place with no discernible pattern whatsoever, then there is no correlation at all between the two variables of the scatter diagram. An example of a scatter diagram that shows no correlation is shown in Figure 1.

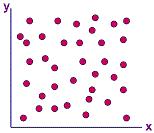
Figure 1. A Scatter Diagram showing no correlation

There is positive correlation between two sets of data if an increase in the x-value results in an increase in the y-value. Figure 2a shows a scatter diagram that exhibits positive correlation. Note that in such a correlation, the data points constitute a perceivable diagonal line that goes from the lower left to the upper right corner.

Not all sets of data pairs will exhibit a strong positive correlation, even if an increase in the x-value somehow results generally in an increase in the y-value. An example of this 'weak' type of positive correlation is shown in the scatter diagram of Figure 2b, which is said to exhibit just a 'possible positive correlation.' This scatter diagram still shows a perceivable diagonal line going in the upper right direction, but the points are more spread apart than in a scatter diagram with strong positive correlation.

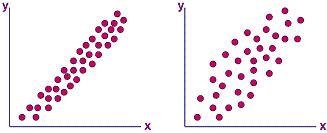
Figure 2. Scatter Diagrams showing positive correlation (a, left) and

just a possible positive correlation (b, right)

If the scatter diagram formed also shows a perceivable diagonal line, but the line is going in a direction opposite that of positive correlation (i.e., from the upper left to the lower right corner) as shown in Figure 3a, then the data pairs are exhibiting negative correlation. This means that y decreases as x increases. Again, the negative correlation is strong if the line formed by the data points is narrow and very defined.

If the negative correlation is not strong, resulting in data points that are not closely packed together, then there is just a 'possible negative correlation.' An example of a scatter diagram for such type of correlation is shown in Figure 3b.

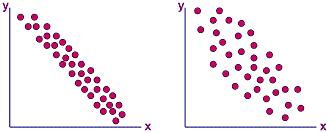
Figure 3. Scatter Diagrams showing negative correlation (a, left) and

just a possible negative correlation (b, right)

Of course, more complex types of correlation may also be identified using a scatter diagram. Once a type of correlation is established, the engineer may choose to proceed with a further and more in-depth investigation of the correlation using other analysis tools.

Determining the exact nature of correlation between variables can lead to benefits. These include: 1) better understanding of cause-effect relationships; 2) reduction of data gathering requirements; 3) establishment of more effective process controls; 4) easier development of check and balance schemes; etc. To realize these benefits, however, the engineer has to use other analytical tools to complement the scatter diagram, since the latter is only used as a quick visual check for possible correlation before a more in-depth study is undertaken.

See Also: Matrix Diagram; Ishikawa Diagram

HOME