Operational Amplifiers; Op-Amps

Operational Amplifiers (Op Amps)

An Operational Amplifier, or Op Amp, is a dual-input, single-output linear amplifier that exhibits a high open-loop gain, high input resistances, and a low output resistance. One of the inputs of an operational amplifier amp is non-inverting while the other is inverting. The output V_out of an operational amplifier without feedback (also known as open-loop) is given by the formula: V_out = A(Vp-Vn) where A is the open-loop gain of the op amp, Vp is the voltage at the non-inverting input, and Vn is the voltage at the inverting input. The open-loop gain of a typical op amp is in the range of 10⁵-10⁶.

The operational amplifier got its name from the fact that it can be configured to perform many different mathematical operations. Depending on its feedback circuit and biasing, an op amp can be made to add, subtract, multiply, divide, negate, and, interestingly, even perform calculus operations such as differentiation and integration. Of course, aside from these operations, op amps are also found in a very large number of applications. In fact, many consider the op amp as the foundation of many analog semiconductor products today.

Because of the very high resistance exhibited by the inputs of an op amp, the currents flowing through them are very small. The current flowing in or out of an op amp's input pin, known as input bias current, is basically just leakage current at the base or gate of the input transistor of that input, which is why it is very small.

When solving voltage/current equations for op amp circuits, the input currents are usually assumed to be zero. For most of the commonly-used op-amp circuits, this means that the total output current of the op amp is flowing through the feedback circuit between the output and the inverting input (the feedback is usually connected to the inverting input for operation stability).

As the main path for an op amp's output current, the feedback circuit used in an op amp largely determines how the op amp will function. There are many ways to operate an op amp, but one commonly-used basic configuration is to: 1)

provide it with balanced supply voltages (say, +/-15V, although single-supply operation is also commonly used); 2) connect the non-inverting input to ground (either directly or with a passive element such as a resistor); 3) connect a feedback circuit between the output and the inverting input; and 4) connect a resistor between the inverting input and the input signal source.

Figure 1 shows some op amp circuits using this basic configuration.

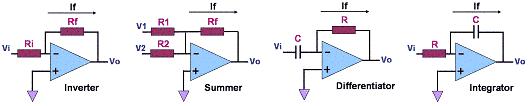
Figure 1. Some Common Operational Amplifier Circuits

Another special characteristic of a close-looped op amp with negative feedback is the zero voltage drop across its inputs. Thus, in the circuits above, the voltage at the inverting input is zero, in effect putting the inverting input at a 'virtual ground.' Table 1 shows the voltage/current equations governing the circuits in Figure 1 above, based on the assumptions that the currents flowing through the op amp inputs and the voltage across them are zero.

Table 1. Voltage/Current Equations for the Op Amp Circuits in Figure 1

Inverting Amplifier

Summer

Differentiator

Integrator

Vo = - If(Rf);

Vi = If(Ri);

Vo = - (Rf/Ri) Vi

Vo = - If(Rf);

If = V1/R1 + V2/R2;

Vo = - Rf(V1/R1 + V2/R2)

Vo = - If(Rf);

If = C dVi/dt

Vo = -RfC(dVi/dt)

Vo = -1/C ∫ If dt;

If = Vi/R;

Vo = -1/(RC) ∫ Vi dt;

A typical op-amp is constructed with the following parts: 1) a differential input stage, which consists of a matched pair of bipolar transistors or field effect transistors (FET's) that produce an output that's proportional to the difference between the input signals; 2) an intermediate-gain stage that amplifies the output of the differential input stage; and 3) a push-pull output stage that is capable of delivering a large current to the load, hence the small output impedance.

HOME